Overview
I wanted the fitness challenge to show where you actually are on the journey. The map image has its own coordinate system and the route is a polyline with many segments. The only inputs we assume are: 1.) the total journey distance is 1779 miles, and 2.) the distance from Hobbiton to Bree is 120 miles.
我想在健身挑戰中準確顯示使用者在旅程中的位置。地圖影像有自己的座標系,路線是由許多線段組成的折線。 我們只假設兩個輸入:1)總旅程為 1779 英里 2.) 從霍比屯到布里為 120 英里。
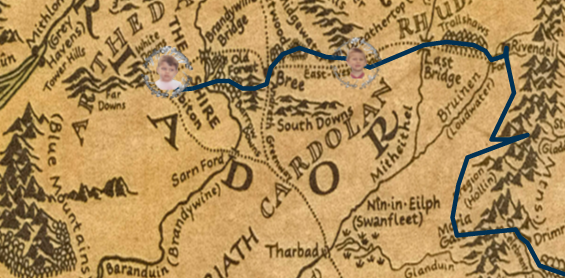
Convert miles to map units
By sampling the Hobbiton to Bree segment we find that 1 mile ≈ 0.62259 map units (for this image/route). A quick sanity check—placing a test user at 120 miles lands them in Bree.
透過取樣霍比屯到布里的路段,我們得到 1 英里 ≈ 0.62259 地圖單位。將測試用戶設為 120 英里時, 會落在布里,驗證無誤。
Which segment am I on?
Let d be the user’s total distance traveled (in miles). Convert to map units with
dUnits = d × 0.62259. Walk the route’s segments, accumulating their lengths in map units until
the cumulative length exceeds dUnits—that segment is the one the user is on.
設使用者總里程為 d 英里,轉換為地圖單位 dUnits = d × 0.62259。依序累加各段長度,
當累積長度超過 dUnits 時,該段即為使用者所在的線段。
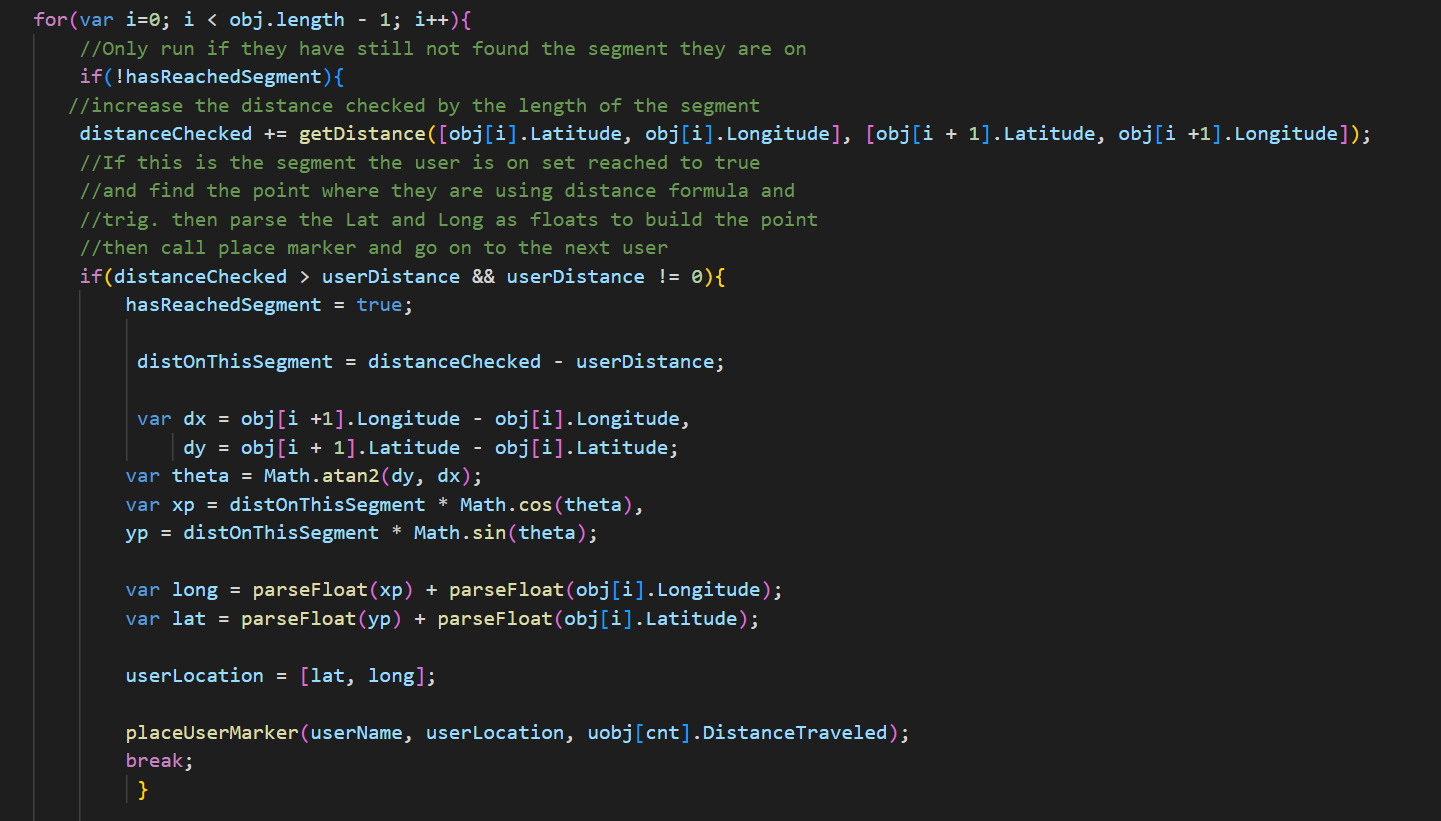
Place the point with trig
With the segment’s start (x₁,y₁) and end (x₂,y₂), compute
θ = atan2(y₂−y₁, x₂−x₁). The user’s offset along that segment is
t = (dUnits − cumulativeBefore) / segmentLength. Then:
ux = x₁ + t · (x₂ − x₁)
uy = y₁ + t · (y₂ − y₁)
You can also think of it using Euler / unit-vector components with cos θ and sin θ.
A refresher: Euler’s formula.
已知線段起點 (x₁,y₁) 與終點 (x₂,y₂),先算
θ = atan2(y₂−y₁, x₂−x₁)。使用者在該段上的比例
t = (dUnits − 累積長度) / 該段長度,則
(ux, uy) 如上式。也可用單位向量
(cos θ, sin θ) 的觀點理解。